دسته بندی های ارشیو: نمونه سوال


نمونه سوال تئوری های پیشرفته مدیریت
نگاه کوتاه
از ویکیپدیا، دانشنامهٔ آزاد
نظریه یا تئوری یا نگره به تفکر انتزاعی یا تعمیمدهنده به شکل اندیشمندانه یا منطقی و یا به نتیجهٔ چنین تفکری اطلاق میشود. بسته به متن، ممکن است نتایج آن تفکر مثلاً توضیح کلی چگونگی عملکرد طبیعت را هم شامل شود. نظریه با فرضیه یکسان نیست. نظریه چارچوبی توضیحدهنده برای یک مشاهده فراهم میآورد و با فرض صحت آن توضیحات، فرضیههای محتملی از پیاش میآیند که میتوان آزمودشان و به صحت یا سقم نظریه پی برد.
در تعاریف جدید بر ذات تفسیری، انتزاعی، و تعمیمدهندگی نظریه تأکید میشود. فیالمثل در هنر و فلسفه، ممکن است از اصلاح «نظری» برای توصیف ایدهها و پدیدههایی تجربی استفاده کنند که بهسادگی قابل اندازهگیری (رؤیت) نباشند. نظریه منتزع و مجرد است (یعنی اضافات و جزئیات نامهم حذف شده و از جسم و ماده منزه است). نظریه با تعیین و تجربه منافات دارد (یعنی عمومیت دارد و به مورد خاصی اشاره ندارد).
نظریه میتواند هنجاربنیاد (یا تجویزی) باشد بدین معنی که دربارهٔ «آنچه باید باشد» توضیح دهد. چنین نظریاتی مبین «اهداف، هنجارها، و استانداردها» هستند. همچنین نظریه میتواند «تودهای از اطلاعات» باشد که به مدلهای توضیحدهندهٔ خاصی مربوط هستند یا نیستند. نظریهپردازی یعنی سروسامان دادن به و پیشبردن این توده از اطلاعات.
همانطور که در تعاریف ارسطو آمده، نظریه اغلب در تقابل با «عمل» است. علت این تقابل این است که نظریهٔ محض شامل هیچ عملی نمیشود جز خودش (خود نظریهپردازی). حوزهٔ پزشکی مثالی آموزنده برای تبیین تفاوتهای «نظری» و «عملی» است: نظریات پزشکی شامل تلاش برای فهم علل و ذات سلامتی و بیماری است، حال آنکه جنبهٔ عملی پزشکی به تلاش برای معالجهٔ بیماران میپردازد. این دو به هم مربوطند اما میتوانند مستقل از یکدیگر باشند چرا که میتوان به پژوهش پیرامون سلامتی و بیماری پرداخت بدون آنکه بیماران را معالجه کرد و نیز ممکن است که بیماری را معالجه کرد بدون آنکه دقیقاً دانست چگونه این معالجه مؤثر واقع شدهاست.
در علم جدید، منظور از اصطلاح «نظریه»، نظریهٔ علمی است. نظریهٔ علمی توضیح مستدل تصدیقشدهای از طبیعت است که با روش علمی سازگار است و معیارهای مورد نیاز علم جدید را ارضا میکند. این نظریات به گونهای توصیف میشوند که هر یک از اهالی فن میتواند درکشان کند و قادر است به روش تجربی اثبات یا ابطالشان کند. نظریات علمی قابل اتکاترین، دقیقترین و جامعترین نوع از اطلاعات علمی هستند که البته این در تناقض با استفادهٔ عوام از واژهٔ «نظریه» به معنای «اثباتنشده» یا «در حد حدس و گمان» است. نظریات علمی با فرضیات و نیز قوانین علمی فرق دارند. همانطور که گفته شد فرضیهها گمانهزنیهایی هستند که به روش تجربی قابل آزمایشاند و قوانین علمی گزارشهای توصیفی دربارهٔ چگونگی عملکرد طبیعت تحت شرایط خاصی هستند.
مدیریت علمی از اواخر قرن سیزدهم هجری شمسی مقارن با اواخر قرن نوزدهم میلادی، گروهی تلاش کردهاند اصول مدیریت را با به کارگیری روشهای مهندسی در طراحی شغل علمیتر سازند. این گروه تلاش خود را بر طراحی اثر بخشی کارکنان متمرکز کردهاند. در واقع جستجو در جهت یافتن روشهای اثربخش و کارا در سازمانها موجب ظهور مکتب کلاسیک در مدیریت شد که به تدوین مدیریت علمی به دست فردریک وینسلو تیلور انجامید این مکتب بر نگرش سازمانی بر مبنای تقسیم کار و تخصص، با توجه به سلسله مراتب اداری تأکید دارد. وی مدیریت علمی را تحت چهار اصل ارائه کرده است.
نظریه زد یا تئوری Z (به انگلیسی: Theory Z)، یکی از تئوریهای مدیریت است که در آن ویژگیهای غالب سازمانهای ژاپنی با ویژگیهای سازمانهای آمریکایی آمیخته شده است. تئوری زد با عنوان “تئوری مدیریت ژاپنی” نیز شناخته میشود.
این نظریه توسط ویلیام اوچی در سال ۱۹۸۱ ارائه شد.[۱][۲]
تئوری تناسب با زمان (به انگلیسی: T-symmetry) در فیزیک نظری تناسب با زمان، تئوریی در بررسی تقارن قوانین فیزیکی در دگرسازی حاصل از بازگشت زمان به گذشته (سفر به گذشته)است.
اگرچه در برخی زمینه ها می توان از تناسب در قوانی فیزیکی دو زمان یافت ولی با توجه به مشاهدات دیداری در دنیای پیرامون بازگشت به زمان گذشته با قوانین فیزیکی چون نیروی هستهای ضعیف و قانون دوم ترمودینامیک تناسب نداشته و نقص میشوند.
تحقیق ارجگزار همانطور که بوشه[۱] (۲۰۱۳) میگوید: «تحقیق ارجگزار روشی است برای مطالعه و تغییر سیستمهای اجتماعی اعم از گروهها، سازمانها و جوامع که از یک مطالعهٔ جمعی به منظور دستیابی به بهترین نظمی که امکان تصور شدن را دارد. این روش بهوسیلهٔ طراحی جمعی از یک آیندهٔ مورد علاقه که اقناعکننده است و بنابراین نیاز به تشویق، اجبار و متقاعد ساختن برای اتفاق افتادن تغییرات برنامهریزی شده ندارد، دنبال میشود.» این مفهوم از اواسط ۱۹۸۰، در ابتدا بهوسیلهٔ دانشجویان و دانشکدهٔ واحد رفتار سازمانی در دانشگاه “کیس وسترن ریزرو” توسعه و گسترش یافت و رشتهٔ توسعه سازمان را بهطور بنیادین تغییر داد و منادی رشتهٔ مطالعات سازمانی اثباتی و جنبش قدرت بنیاد در مدیریت آمریکایی بود. مقالهٔ بنیادی ۱۹۸۷ دیوید کوپرریدر و سورش اسریواستوا دربارهٔ این موضوع بحث میکند که استفاده بیش از اندازه از روش حل مسئله، از توانایی مدیران و پژوهشگران برای بهره بردن از نظریههای جدید و مدلهای سازماندهیکردن کاستهاست. [۲] با بکار بستن یک روش ساختارگرای اجتماعی، که معتقد است سازمانها بهوسیلهٔ گفتگوها بهوجود میآیند، باقی میمانند و تغییر میکنند، آنها به این واقعیت اشاره کردند؛ که روشهای ما برای سازماندهی تنها بهوسیلهٔ تصورات مردم و توافقهای میان آنان محدود میشوند. [۳] تاریخ تحقیق ارجگزار توسط گرواس بوشه در مقالهای درباره تحقیق ارجگزار در سال ۲۰۱۲ توصیف شدهاست. آشکار شدن موفقیت روش تحقیق ارجگزار در GTE در میانهٔ دههٔ نود منجر به تماسهایی با کوپر ریدر برای انتشار یک کتاب راهنما به نام ” چگونه” شد. که در آن او دربارهٔ چیزی که سالها بر آن اصرار کرده بود؛ یعنی درخواست از مردم برای تمرکز بر تئوری و خلاقیت داشتن در برخورد با روشها سخن گفته بود. در نتیجهٔ کار کوپر رویکردهای متفاوت بسیاری به تحقیق ارجگزار در سراسر جهان رشد کردند.
اصول متد تحقیق ارجگزار
روش تحقیق ارجگزار بر این فرض مبتنی است که سوالهایی که ما میپرسیم، تمایل دارند که توجه ما را به مسیر خاصی متمرکز کنند. برخی از روشهایی که در پی برآورده و ارزیابی کردن یک موقعیت و سپس ارائهٔ راه حل برای آن هستند، بر مدل ناکاراندی استوار هستند. برخی دیگر از رویکردها هم چنین سوالهایی را میپرسند: مشکلات کدام هستند؟ چه چیزی اشتباه است؟ چه چیزی به تعمیر و اصلاح نیاز دارد. به جای این پرسش که چه چیزی اشباه است؟ برخی روشهای دیگر پرسش را درلفافهای از اصطلاحات چالش برانگیز میپوشانند. رویکرد تحقیق ارجگزار استدلال میکند که این شیوهٔ برخورد نیز بنیانهای ناکارامدی را در درون خود نگاه میدارد. تفکری که پشت این سوال است این است که چیزهای اشتباهی وجود دارند، یا اینکه چیزهایی به تعمیر و اصلاح نیاز دارند. [۴] در سال ۱۹۹۰ دیوید کوپرایدر و دایانا ویتنی مقالهای را منتشر کردند که در آن پنج اصل کلی تحقیق ارجگزار ترسیم شده بود. اصولی که تبدیل به مدل استانداردی برای استفاده محققین و پزشکان شد. [۵] توضیح زیر از دائرهالمعارف تئوری مدیریت سیج (Sage) گرفته شده است: [۱] ۱) اصل ساختارگرا: پیشنهاد میکند که؛ آنچه ما به درستی آن معتقدیم، تعیین کنندهٔ کاری است که ما انجام میدهیم و اندیشه و عمل در روابط شان است که پدیدار میشوند. مردم به وسیلهٔ زبان و گفتمان تعاملات روزمرهٔ خود، سازمانهایی را که در آن مستقر هستند بازتولید میکنند. هدف تحقیق ارجگزار تشویق ایدههای جدید و داستانها وتصاویر است که امکانهای تازهای را برای کنش تولید کنند. ۲) اصل همزمانی: پیشنهاد میکند که؛ همینکه ما وارد تحقیق در سیستمهای انسانی میشویم، در عین حال این سیستمها را تغییر نیز میدهیم و بذرهای تغییر، یعنی چیزهایی که مردم دربارهٔ آن فکر میکنند و حرف میزنند، چیزهایی که انها جستجو میکنند و یاد میگیرند، در واقع به طور تلویحی در اولین پرسشها وجود دارند. پرسشها هیچگاه بدیهی و طبیعی نیستند، انها سرنوشت سازند و سیستمهای اجتماعی در مسیر پرسشهایی حرکت میکنند که به اصرار و با حرارت در آن جوامع مورد بحث قرار میگیرند.
۳) اصل شاعرانه: پیشنهاد میکند که زندگی سازمانی در داستانهایی که مردم هر روزه برای هم تعریف میکنند بیان میشود، داستان یک سازمان به طور مداوم به وسیلهٔ مردم بازآفرینی میشود. واژهها و موضوعاتی که برای تحقیق انتخاب میشوند، تاثیری ورای خود کلمات دارند. آنها احساسات، فهمها و جهانهای معنا را احضار کرده و مورد خطاب قرار میدهند. در همهٔ مراحل تحقیق، تلاشها باید در جهت استفاده از واژههایی باشد که در جهت زندگی بخشیدن و الهام بخشیدن به بهترینها در مردم باشد.
۴) اصل پیش بینی: فرض میکند تصوری که ما از آینده داریم راهنمای کارهایی است که امروز انجام میدهیم. سیستمهای انسانی پیوسته افقی از انتظارات را در مقابل خود طرح ریزی میکنند که به شکل قدرتمندی آینده را به حال میآورد و به مثابه یک عامل بسیج، عمل میکند. تحقیق ارجگزار از آفرینش هنرمندانهٔ تصویر سازی مثبت بر پایههای جمعی به منظور بازسازی واقعیت پیش بینی استفاده میکند.
۵) اصل مثبت: پیشنهاد میکند حرکت و تغییر مداوم به احساسات مثبت و پیومند اجتماعی نیاز دارد. احساساتی مانند امید، هیجان، روحیه، رفاقت و شادی باعث زیاد شدن خلاقیت، گشودگی به روی ایدهها و مردم جدید و انعطافپذیری شناختی میشوند. آنها همچنین ارتباطات و روابط قوی بین مردم را ترویج میکنند. مخصوصا بین گروههایی که در حال منازعه هستند و به تحقیق و تغییر جمعی نیاز دارند.
بعضی پژوهشگران معتقدند که تمرکز بیش از حد بر روی اختلالات میتواند در واقع سبب بدتر شدن آنها و شکست آنها در بهتر شدن شود. [۶] در مقابل تحقیق ارجگزار استدلال میکند وقتی که همهٔ اعضای یک سازمان به فهمیدن و ارزش قائل شدن برای ویژگیهای مطلوب فرهنگ خودشان تشویق شوند، یک بهبود سریع در سازمان به وجود میآید. [۷] روشهای مبتنی بر قدرت در ایجاد استراتژی توسعه سازمانی و اجرای تاکتیکهای اثربخشی سازمانی مورد استفاده قرار گرفتهاند. وجه ارجگزار نه یک تحقیق عمدتاً متکی بر مصاحبههایی برای درک کیفی تواناییها و استعدادهای بالقوه سازمان به وسیلهٔ جستجو کردن در تجربه و پتانسیلهای سازمان است: هدف روشن ساختن داشتهها و انگیزههای شخصی است که قدرت آن سازمان هستند. بوشه در سلسله مقالات پرنفوذی استدلال کرده است که جریان اصلی هواداران تحقیق ارجگزار توجه خود را بیش از حد بر “امر مثبت” متمرکز کرده و به اندازهٔ کافی به خلاقیت و پویایی آزاد شده به وسیلهٔ تحقیق ارجگزار توجه نکردهاند. ([۹][۱۰][۱۱]) در مطالعهٔ تطبیقی که در سال ۲۰۱۰ در حوزهٔ مدرسه صورت گرفت او متوجه شد که حتی در مواردی که هیچ تغییری اتفاق نیفتاده بود، شرکت کنندگان در فرایند تحقیق ارجگزار بسیار مثبت بودند. چیزی که موقعیتهایی را که تغییرات تحولی را تجربه کردهاند متمایز میکرد، ایجاد ایدههای جدیدی بود که به مردم راههای جدیدی را برای رصد کرد مسائل قدیمی ارائه میکرد. او استدلال کرد برای اینکه تغییرات تحولی اتفاق بیفتد، تحقیق ارجگزار باید مشکلاتی را رصد کند که مردم آنقدر دربارهشان نگران هستند که میخواهند آنها را تغییر دهند. با این وجود تحقیق ارجگزار این مسائل را نه از طریق رویکرد حل مساله بلکه از طریق تصورهای آفریننده حل میکند. [۱۲] بوشه و دکتر روان فری از دانشگاه کیس وسترن رزرو در یک ویدئوی ۹۰ دقیقهای مقولات مثبت بودن و آفرینشگر بودن را در کنفرانس جهانی تحقیق ارجگزار مورد بحث قرار دادهاند که از اینجا قابل دسترس است. اخیرترین بررسی دانشگاهی از تحقیق ارجگزار ۱۰ پروسهٔ تغییر را که در تحقیق ارجگزار تعبیه شده است توضیح میدهد. نقدهای اخیر و شواهد پژوهشی در اینجا قابل دسترس است.
رئوس مطالب
دو دیدگاه درتعریف مدیریت – ماهیت و خصوصیات مدیریت – محدوده مدیریت – نواحی عملیاتی مدیریت -نقش های مدیریت – مدیران اثر بخش ، مدیران موفق – توزیع زمان در فعالیت مدیران اثربخش، موفق و متوسط – توزیع سازمان بر حسب وظیفه در سطح سازمانی – شایستگی های مدیریت – تعریف سازمان – طرح سازمانی (چارت سازمانی) -ساختارسازمانی (ویژه گیها) – دیدگاه سازمانی – ویژه گیهای یک سیستم باز – دیدگاه چرخه حیات به سازمان – دلایل اهمیت سازمان – تئوری چیست – اثربخش سازمان – ابعاد ساختار سازمانی – مدیریت کارآفرینی – طراحی شغل – مدیریت دانش – مدیریت کیفیت – مدیریت تعارض – مدیریت استعداد – مدیریت سرمایه

نمونه سئوال کتاب مدیریت بازاریابی
نگاه کوتاه
بر اساس تعریف فیلیپ کاتلر، مدیریت بازاریابی عبارت است از فرایند برنامهریزی و اجرای پندار توزیع ایده، کالا و خدمات به قصد انجام مبادلاتی که به تامین اهداف انفرادی و سازمانی منجر گردد. برخلاف استنباط سطحی رایج، که مفهوم بازاریابی را ایجاد تقاضا برای محصول میداند، بازاریابی به طیف وسیعی از فعالیتها اطلاق میگردد که از تحقیقات بازاریابی، برنامهریزی، اجرا و کنترل تقاضا تشکیل شده است. مدیر بازاریابی، در چارچوب برنامهی بازاریابی، در مورد بازارهای هدف، تولید کالای جدید، قیمتگذاری، کانالهای توزیع کالا، ارتباطات، برندسازی و تبلیغات، فعالیت های لازم برای رسیدن به اهداف سازمانی را ساماندهی و هدایت میکند. [۲] همانطور که از تعریف برمی آید، بازاریابی امری ست که در جهت برنامه ریزی نحوه حضور در بازارهای هدفگیری شده برای محصولات/خدماتنقشی پررنگتر ایفا می کند. اما باید توجه داشته باشیم، امر برنامه ریزی کردن صرفاً نوشتن چند بند از وظایف و مشخص کردن زمان انجام آنها نیست، بلکه وجود یک تیم اجرایی قوی در این زمینه بسیار مهم است. البته می توان به این نکته نیز اشاره کرد که وجود تیم هایی که میزان فاصله سازمان یا یک واحد خاص را با ارائه گزارش های دوره ای و مدیریتی مورد بررسی قرار می دهند نیز حائز اهمیت است. به روشنی از تعاریف بالا مشخص است، واحد بازاریابی کاری فراتر از فروش و جذب مشتری دارد. و این دو بخش کوچکی از کارهای عمده واحد بازاریابی محسوب می شود.
رئوس مطالب
بازاریابی جدید از نظر فیلیپ کاتلر -نیازها و خواسته ها – مبادله در تعریف بازاریابی – تعریف بازار و اندازه بازار – ابعاد گوناگون مارکتینگ – بازارگرائی – بازارشناسی – بازارسازی – بازارگردی – آمیخته بازاریابی – بازارسنجی – بازارداری و بازارگرمی – مدیریت بازاریابی – انواع تقاضا – تقاضای منفی و بازاریابی تبدیلی – تقاضای پنهان – گرایش محصول در فلسفه مدیریت بازاریابی – گرایش فروش – گرایش بازاریابی – مهمترین اجزای سیستم بازار – فرایند تصمیم گیری خرید مصرف کننده – عوامل موثر در فرایند تصمیم گیری – عوامل مربوط به آمیخته بازاریابی – راه های کسب موفقیت در بازاریابی الکترونیکی – اصول افزایش فروش در اینترنت – راه های موثر درکاهش هزینه کسب و کار – چارچوب کلی نوشتن برنامه بازاریابی – ابعاد مختلف پژوهشهای بازاریابی – انواع محیط در بازاریابی الکترونیکی – مدیریت زنجیره تأمین – نقش موثر سیستم های اطلاعاتی در فرایند های رقابتی بازار – ویژگی های مهم یک میزبان خوب – جنبه های قوانین حقوقی در طراحی سایتهای تجارت الکترونیک – راهبردهای تبلیغی در سایتها – برند سازی در کسب و کار

مرور برخی مباحث ریاضیات مهندسی
ریاضیات
ریاضیات (در قدیم[نیازمند منبع]، همچنین: اِنگارِش[۱]) را بیشتر دانش بررسی کمیتها و ساختارها و فضا و دگرگونی (تغییر) تعریف میکنند. دیدگاه دیگری ریاضی را دانشی میداند که در آن با استدلال منطقی از اصول و تعریفها به نتایج دقیق و جدیدی میرسیم (دیدگاههای دیگری نیز در فلسفه ریاضیات بیان شدهاست). با اینکه ریاضیات از علوم طبیعی به شمار نمیرود، ولی ساختارهای ویژهای که ریاضیدانان میپژوهند بیشتر از دانشهای طبیعی بهویژه فیزیک سرچشمه میگیرند و در فضایی جدا از طبیعت و محضگونه گسترش پیدا میکنند، بهطوری که علوم طبیعی برای حل مسائل خود به ریاضی باز میگردند تا جوابشان را با آن مقایسه و بررسی کنند.
علوم طبیعی، مهندسی، اقتصاد و پزشکی بسیار به ریاضیات تکیه دارد ولی ریاضیدانان گاه به دلایل صرفاً ریاضی (و نه کاربردی) به تعریف و بررسی برخی ساختارها میپردازند.
تاریخچه
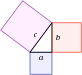
مصریان باستان، بیش از ۵ هزار سال پیش، برای اندازهگیری و نقشهبرداری زمین و ساختن اهرام با دقت بسیار بالا، از حساب و هندسه استفاده میکردند. علم حساب با اعداد و محاسبه سر و کار دارد. در حساب، چهار عمل اصلی عبارتند از: جمع، تفریق، ضرب و تقسیم. هندسه علم مطالعه خطها، زاویهها، شکلها، و حجمها است. یونانیهایی چون اقلیدس، حدود ۲۵۰۰ سال قبل، بیشتر قوانین اصلی هندسه (قضایای هندسه) را تعیین کردند. جبر نوعی خلاصهنویسی ریاضیات است که در آن برای نشان دادن کمّیتهای نامعلوم، از علائمی چون x و y استفاده میشود. این علم را نیز دانشمندان ایرانی، حدود ۱۲۰۰ سال قبل توسعه دادند. حساب، هندسه و جبر، پایههای ریاضیات هستند.
ریاضیات نوعی زبان علمی است. مهندسان، فیزیکدانان، و سایر دانشمندان، همگی از ریاضیات در کارهایشان استفاده میکنند. سایر کارشناسان که به مطالعه اعداد، کمّیتها، شکلها و فضا بهشکل محض علاقه دارند، ریاضیات محض (غیرکاربردی) را به کار میگیرند. نظریه اعداد که شامل مطالعه اعداد درست و نحوه عمل آنهاست، شاخهای از ریاضیات محض به شمار میآید. در دنیای جدید، ریاضیات یکی از عناصر کلیدی علوم الکترونیک و رایانه بهشمار میرود.
کمیت
مجموعه، رابطه، تابع، عمل، گروه، میدان، عدد، اعداد طبیعی، اعداد حسابی، اعداد صحیح، اعداد اول، اعداد مرکب، اعداد گویا، اعداد گنگ، اعداد حقیقی، اعداد مختلط، اعداد جبری، عدد پی، عدد ای، چهارگانها، هشتگانها، شانزدگانها، اعداد پی-ادیک، اعداد فوق پیچیده (Hypercomplex numbers)، اعداد فوق حقیقی (Hyperreal number)، اعداد فراواقعی (Surreal numbers)، بینهایت، اعداد ترتیبی، اعداد اصلی، ثابتهای ریاضی، پایه
ساختار
جبر مجرد، نظریه اعداد، هندسه جبری، نظریه گروهها، مونوئیدها، آنالیز ریاضی، آنالیز تابعی، توپولوژی، جبر خطی، نظریه گراف، جبر عمومی، نظریه مدولها، نظریه ترتیب، [[نظ
فضا
توپولوژی، هندسه، مثلثات، هندسه جبری، هندسه دیفرانسیل، توپولوژی دیفرانسیل، توپولوژی جبری، جبر خطی، هندسه برخالها، متری
تغییر
حساب، حسابان، حساب برداری، آنالیز ریاضی، معادلات دیفرانسیل، سیستمهای دینامیکی، نظریه آشوب، فهرست تابعها
پایهها و روشهای ریاضیات
فلسفه ریاضیات، شهودگرایی، ساختگرائی، مبانی ریاضیات، نظریه مجموعهها، منطق نمادی، نظریه مدل، نظریه رستهها، منطق ریاضی، ریاضیات معکوس، جدول نمادهای ریاضی
ریاضیات گسسته
ترکیبیات، نظریه شهودی مجموعهها، نظریه رایانش، رمزنگاری، نظریه گراف
ریاضیات کاربردی
فیزیک ریاضی، مکانیک، مکانیک سیالات، آنالیز عددی، بهینهسازی، احتمالات، آمار، اقتصاد ریاضی، ریاضیات مالی، نظریه بازیها، ریاضیات زیستی، رمزنگاری، نظریه اطلاعات
گفتاورد (نقل قول)
برتراند راسل زمانی که دربارهٔ روش بُنداشتی (اصل موضوعی) سخن میگفت که در آن برخی ویژگیهای یک ساختار (که چیزی از آن نمیدانیم) فرض میشود و پیامدهای این فرض از راه منطق نتیجهگیری میشود گفت:
ریاضیات را میتوان رشتهای تعریف کرد که در آن نه معلوم است از چه سخن میگوییم و نه میدانیم آنچه میگوییم صحت دارد.
ما در ریاضیات مطالب را نمیفهمیم، بلکه تنها به آنها عادت میکنیم.

ریاضیات گسسته
ریاضیات
ریاضیات (در قدیم[نیازمند منبع]، همچنین: اِنگارِش[۱]) را بیشتر دانش بررسی کمیتها و ساختارها و فضا و دگرگونی (تغییر) تعریف میکنند. دیدگاه دیگری ریاضی را دانشی میداند که در آن با استدلال منطقی از اصول و تعریفها به نتایج دقیق و جدیدی میرسیم (دیدگاههای دیگری نیز در فلسفه ریاضیات بیان شدهاست). با اینکه ریاضیات از علوم طبیعی به شمار نمیرود، ولی ساختارهای ویژهای که ریاضیدانان میپژوهند بیشتر از دانشهای طبیعی بهویژه فیزیک سرچشمه میگیرند و در فضایی جدا از طبیعت و محضگونه گسترش پیدا میکنند، بهطوری که علوم طبیعی برای حل مسائل خود به ریاضی باز میگردند تا جوابشان را با آن مقایسه و بررسی کنند.
علوم طبیعی، مهندسی، اقتصاد و پزشکی بسیار به ریاضیات تکیه دارد ولی ریاضیدانان گاه به دلایل صرفاً ریاضی (و نه کاربردی) به تعریف و بررسی برخی ساختارها میپردازند.
تاریخچه
مصریان باستان، بیش از ۵ هزار سال پیش، برای اندازهگیری و نقشهبرداری زمین و ساختن اهرام با دقت بسیار بالا، از حساب و هندسه استفاده میکردند. علم حساب با اعداد و محاسبه سر و کار دارد. در حساب، چهار عمل اصلی عبارتند از: جمع، تفریق، ضرب و تقسیم. هندسه علم مطالعه خطها، زاویهها، شکلها، و حجمها است. یونانیهایی چون اقلیدس، حدود ۲۵۰۰ سال قبل، بیشتر قوانین اصلی هندسه (قضایای هندسه) را تعیین کردند. جبر نوعی خلاصهنویسی ریاضیات است که در آن برای نشان دادن کمّیتهای نامعلوم، از علائمی چون x و y استفاده میشود. این علم را نیز دانشمندان ایرانی، حدود ۱۲۰۰ سال قبل توسعه دادند. حساب، هندسه و جبر، پایههای ریاضیات هستند.
ریاضیات نوعی زبان علمی است. مهندسان، فیزیکدانان، و سایر دانشمندان، همگی از ریاضیات در کارهایشان استفاده میکنند. سایر کارشناسان که به مطالعه اعداد، کمّیتها، شکلها و فضا بهشکل محض علاقه دارند، ریاضیات محض (غیرکاربردی) را به کار میگیرند. نظریه اعداد که شامل مطالعه اعداد درست و نحوه عمل آنهاست، شاخهای از ریاضیات محض به شمار میآید. در دنیای جدید، ریاضیات یکی از عناصر کلیدی علوم الکترونیک و رایانه بهشمار میرود.
کمیت
مجموعه، رابطه، تابع، عمل، گروه، میدان، عدد، اعداد طبیعی، اعداد حسابی، اعداد صحیح، اعداد اول، اعداد مرکب، اعداد گویا، اعداد گنگ، اعداد حقیقی، اعداد مختلط، اعداد جبری، عدد پی، عدد ای، چهارگانها، هشتگانها، شانزدگانها، اعداد پی-ادیک، اعداد فوق پیچیده (Hypercomplex numbers)، اعداد فوق حقیقی (Hyperreal number)، اعداد فراواقعی (Surreal numbers)، بینهایت، اعداد ترتیبی، اعداد اصلی، ثابتهای ریاضی، پایه
ساختار
جبر مجرد، نظریه اعداد، هندسه جبری، نظریه گروهها، مونوئیدها، آنالیز ریاضی، آنالیز تابعی، توپولوژی، جبر خطی، نظریه گراف، جبر عمومی، نظریه مدولها، نظریه ترتیب، [[نظ
فضا
توپولوژی، هندسه، مثلثات، هندسه جبری، هندسه دیفرانسیل، توپولوژی دیفرانسیل، توپولوژی جبری، جبر خطی، هندسه برخالها، متری
تغییر
حساب، حسابان، حساب برداری، آنالیز ریاضی، معادلات دیفرانسیل، سیستمهای دینامیکی، نظریه آشوب، فهرست تابعها
پایهها و روشهای ریاضیات
فلسفه ریاضیات، شهودگرایی، ساختگرائی، مبانی ریاضیات، نظریه مجموعهها، منطق نمادی، نظریه مدل، نظریه رستهها، منطق ریاضی، ریاضیات معکوس، جدول نمادهای ریاضی
ریاضیات گسسته
ترکیبیات، نظریه شهودی مجموعهها، نظریه رایانش، رمزنگاری، نظریه گراف
ریاضیات کاربردی
فیزیک ریاضی، مکانیک، مکانیک سیالات، آنالیز عددی، بهینهسازی، احتمالات، آمار، اقتصاد ریاضی، ریاضیات مالی، نظریه بازیها، ریاضیات زیستی، رمزنگاری، نظریه اطلاعات
گفتاورد (نقل قول)
برتراند راسل زمانی که دربارهٔ روش بُنداشتی (اصل موضوعی) سخن میگفت که در آن برخی ویژگیهای یک ساختار (که چیزی از آن نمیدانیم) فرض میشود و پیامدهای این فرض از راه منطق نتیجهگیری میشود گفت:
ریاضیات را میتوان رشتهای تعریف کرد که در آن نه معلوم است از چه سخن میگوییم و نه میدانیم آنچه میگوییم صحت دارد.
ما در ریاضیات مطالب را نمیفهمیم، بلکه تنها به آنها عادت میکنیم.

آمار و احتمالات
آمار
به مجموعهٔ دادههای عددی مربوط به یک موضوع (معمولاً مهم)، مانند جمعیت، متوفیات، میزان تجارت داخلی یا خارجی، دما یا بارش ماهیانه و غیر گفته میشود. آمار را باید علم و عمل استخراج، بسط، و توسعهٔ دانشهای تجربی انسانی با استفاده از روشهای گردآوری، تنظیم، پرورش، و تحلیل دادههای تجربی (حاصل از اندازهگیری و آزمایش) دانست. زمینههای محاسباتی و رایانهای جدیدتری همچون یادگیری ماشینی، و کاوشهای ماشینی در دادهها، در واقع، امتداد و گسترش دانش گسترده و کهن از آمار به عهد محاسبات نو و دوران اعمال شیوههای ماشینی در همهجا میباشد. علم آمار، علم فن فراهم کردن دادههای کمّی و تحلیل آنها به منظور به دست آورن نتیایجی که اگرچه احتمالی است، اما در خور اعتماد است.
در صورتی که شاخهای علمی مد نظر نباشد، معنای آن، دادههایی بهشکل ارقام و اعداد واقعی یا تقریبی است که با استفاده از علم آمار میتوان با آنها رفتار کرد و عملیات ذکر شده در بالا را بر آنها انجام داد. بیشتر مردم با کلمه آمار به مفهومی که برای ثبت و نمایش اطلاعات عددی به کار میرود آشنا هستند؛ ولی این مفهوم منطبق با موضوع اصلی مورد بحث آمار نیست. آمار عمدتاً با وضعیتهایی سر و کار دارد که در آنها وقوع یک پیشامد به طور حتمی قابل پیش بینی نیست. اسنتاجهای آماری غالباً غیر حتمی اند، زیرا مبتنی بر اطلاعات ناکاملی هستند. در طول چندین دهه آمار فقط با بیان اطلاعات و مقادیر عددی درباره اقتصاد، جمعیتشناسی و اوضاع سیاسی حاکم در یک کشور سر و کار داشت. حتی امروز بسیاری از نشریات و گزارشهای دولتی که تودهای از آمار و ارقام را در بردارند معنی اولیه کلمه آمار را در ذهن زنده میکنند. اکثر افراد معمولی هنوز این تصویر غلط را درباره آمار دارند که آن را منحصر به ستونهای عددی سرگیجه آور و گاهی یک سری شکلهای مبهوت کننده میدانند؛ بنابراین، یادآوری این نکته ضروری است که نظریه و روشهای جدید آماری از حد ساختن جدولهای اعداد و نمودارها بسیار فراتر رفتهاند. آمار به عنوان یک موضوع علمی، امروزه شامل مفاهیم و روشهایی است که در تمام پژوهشهایی که مستلزم جمعآوری دادهها به وسیله یک فرایند آزمایش و مشاهده و انجام استنباط و نتیجهگیری به وسیله تجزیه و تحلیل این دادهها هستند اهمیت بسیار دارند.
علم آمار، مبتنی است بر دو شاخه آمار توصیفی و آمار استنباطی. در آمار توصیفی با داشتن تمام اعضا جامعه به بررسی خصوصیتهای آماری آن پرداخته میشود در حالی که در آمار استنباطی با بدست آوردن نمونهای از جامعه که خصوصیات اصلی جامعه را بیان میکند در مورد جامعه استباط آماری انجام میشود. در نظریهٔ آمار، اتفاقات تصادفی و عدم قطعیت توسط نظریهٔ احتمالات مدلسازی میشوند. در این علم، مطالعه و قضاوت معقول در بارهٔ موضوعهای گوناگون، بر مبنای یک نمونه انجام میشود و قضاوت در مورد یک فرد خاص، اصلاً مطرح نیست.
از جملهٔ مهمترین اهداف آمار، میتوان تولید «بهترین» اطّلاعات از داده های موجود و سپس استخراج دانش از آن اطّلاعات را ذکر کرد. به همین سبب است که برخی از منابع، آمار را شاخهای از نظریه تصمیمها به شمار میآورند.
از طرف دیگر میتوان آن را به دو بخش آمار کلاسیک و آمار بیز تقسیمبندی کرد. در آمار کلاسیک، که امروزه در دانشگاهها و دبیرستانها تدریس میگردد، ابتدا آزمایش و نتیجه را داریم و بعد بر اساس آنها فرضها را آزمون میکنیم. به عبارت دیگر ابتدا آزمایش انجام میشود و بعد فرض آزمون میگردد. در آمار بیزی ابتدا فرض در نظر گرفته میشود و دادهها با آن مطابقت داده میشوند به عبارت دیگر در آمار بیزی یک پیش توزیع داریم-توزیع پیشین- و بعد از مطالعه دادهها و برای رسیدن به آن توزیع پیشین، توزیع پسین را در نظر میگیریم.
مطالعات تجربی و مشاهداتی هدف کلی برای یک پروژه تحقیقی آماری، بررسی حوادث اتفاقی بوده و به ویژه نتیجهگیری روی تأثیر تغییرات در ارزش شاخصها یا متغیرهای غیر وابسته روی یک پاسخ یا متغیر وابستهاست. دو شیوه اصلی از مطالعات آماری تصادفی وجود دارد: مطالعات تجربی و مطالعات مشاهداتی. در هر دو نوع از این مطالعات، اثر تغییرات در یک متغیر (یا متغیرهای) غیر وابسته روی رفتار متغیرهای وابسته مشاهده میشود. اختلاف بین این دو شیوه درچگونگی مطالعهای است که عملاً هدایت میشود. یک مطالعه تجربی در بردارنده روشهای اندازهگیری سیستم تحت مطالعهاست که سیستم را تغییر میدهد و سپس با استفاده از روش مشابه اندازهگیریهای اضافی انجام میدهد تا مشخص سازد که آیا تغییرات انجام شده، مقادیر شاخصها را تغییر میدهد یا خیر. در مقابل یک مطالعه نظری، مداخلات تجربی را در بر نمیگیرد. در عوض داده ها جمعآوری میشوند و روابط بین پیش بینیها و جواب بررسی میشوند.
یک نمونه از مطالعه تجربی، مطالعات Hawthorne مشهور است که تلاش کرد تا تغییرات در محیط کار را در کمپانی الکتریک غربی Howthorne بیازماید. محققان علاقهمند بودند که آیا افزایش نور میتواند کارایی را در کارگران خط تولید افزایش دهد. محققان ابتدا کارایی را در کارخانه اندازهگیری کردند و سپس میزان نور را در یک قسمت از کارخانه تغییر دادند تا مشاهده کنند که آیا تغییر در نور میتواند کارایی را تغییر دهد. به واسطه خطا در اقدامات تجربی، به ویژه فقدان یک گروه کنترل محققاتی در حالی که قادر نبودند آنچه را که طراحی کرده بودند، انجام دهند قادر شدند تا محیط را با شیوه Hawthorne آماده سازند. یک نمونه از مطالعه مشاهداتی، مطالعه ایست که رابطه بین سیگار کشیدن و سرطان ریه را بررسی میکند. این نوع از مطالعه به طور اختصاصی از شیوهای استفاده میکند تا مشاهدات مورد علاقه را جمعآوری کند و سپس تجزیه و تحلیل آماری انجام دهد. در این مورد، محققان مشاهدات افراد سیگاری و غیر سیگاری را جمعآوری میکنند و سپس به تعداد موارد سرطان ریه در هر دو گروه توجه میکنند.
احتمالات
طور ساده، احتمالات (به انگلیسی: Probability) به شانس وقوع یک حادثه گفته میشود.
احتمال معمولاً مورد استفاده برای توصیف نگرش ذهن نسبت به گزاره هایی است که ما از حقیقت انها مطمئن نیستیم. گزاره های مورد نظر معمولاً از فرم “آیا یک رویداد خاص رخ می دهد؟” و نگرش ذهن ما از فرم “چقدر اطمینان داریم که این رویداد رخ خواهد داد؟” است. میزان اطمینان ما، قابل توصیف به صورت عددی می باشد که این عدد مقداری بین ۰ و ۱ را گرفته و آن را احتمال می نا میم. هر چه احتمال یک رویداد بیشتر باشد، ما مطمئن تر خواهیم بود که آن رویداد رخ خواهد داد. درواقع میزان اطمینان ما از اینکه یک واقعه (تصادفی) اتفاق خواهد افتاد.
ظریهٔ احتمالات به شاخهای از ریاضیات گویند که با تحلیل وقایع تصادفی سروکار دارد.
مانند دیگر نظریه ها، نظریه احتمال نمایشی از مفاهیم احتمال به صورت شرایط صوری (فرمولی) است – شرایطی که میتواند به طور جدا از معنای خود در نظر گرفته شود. این فرمولبندی صوری توسط قوانین ریاضی و منطق دستکاری، ونتیجه های حاصله، تفسیر و یا دوباره به دامنه مسئله ترجمه می شوند.
حداقل دو تلاش موفق برای به بصورت فرمول دراوردن احتمال وجود دار : فرمولاسیون کولموگروف و فرمولاسیون کاکس. در فرمولاسیون کولموگروف (نگاه کنیدبه )، مجموعه ها به عنوان واقعه و احتمالات را به عنوان میزانی روی یک سری از مجموعه ها تفسیرمی کنند. در نظریه کاکس، احتمال به عنوان یک اصل (که هست، بدون تجزیه و تحلیل بیشتر) و تاکید بر روی ساخت یک انتساب سازگار از مقادیر احتمال برای گزاره ها است. در هر دو مورد، قوانین احتمال یکی هستند مگر برای جزئیات تکنیکی مربوط به آنها.
روشهای دیگری نیز برای کمی کردن میزان عدم قطعیت، مانند نظریه Dempster-Shafer theory یا possibility theory وجود دارد ، اما آن ها به طور اساسی با آنچه گفته شد، تفاوت دارند و با درک معمول از قوانین احتمال سازگار نیستند.
مطالعه علمی احتمال، توسعه ای مدرن است. قمارنشان می دهد که علاقه به ایده های تعیین کمیت برای احتمالات به هزاران سال می رسد، اما توصیفات دقیق ریاضی خیلی دیرتر به وجود آمد. دلایلی البته وجود دارد که توسعه ریاضیات احتمالات را کند می کند. در حالی که بازی های شانس انگیزه ای برای مطالعه ریاضی احتمال بودند، اما مسائل اساسی هنوز هم تحت تاثیر خرافات قماربازان پوشیده می شود.

ریاضی عمومی-مجموعه کامل
ریاضیات
ریاضیات (در قدیم[نیازمند منبع]، همچنین: اِنگارِش[۱]) را بیشتر دانش بررسی کمیتها و ساختارها و فضا و دگرگونی (تغییر) تعریف میکنند. دیدگاه دیگری ریاضی را دانشی میداند که در آن با استدلال منطقی از اصول و تعریفها به نتایج دقیق و جدیدی میرسیم (دیدگاههای دیگری نیز در فلسفه ریاضیات بیان شدهاست). با اینکه ریاضیات از علوم طبیعی به شمار نمیرود، ولی ساختارهای ویژهای که ریاضیدانان میپژوهند بیشتر از دانشهای طبیعی بهویژه فیزیک سرچشمه میگیرند و در فضایی جدا از طبیعت و محضگونه گسترش پیدا میکنند، بهطوری که علوم طبیعی برای حل مسائل خود به ریاضی باز میگردند تا جوابشان را با آن مقایسه و بررسی کنند.
علوم طبیعی، مهندسی، اقتصاد و پزشکی بسیار به ریاضیات تکیه دارد ولی ریاضیدانان گاه به دلایل صرفاً ریاضی (و نه کاربردی) به تعریف و بررسی برخی ساختارها میپردازند.
تاریخچه
مصریان باستان، بیش از ۵ هزار سال پیش، برای اندازهگیری و نقشهبرداری زمین و ساختن اهرام با دقت بسیار بالا، از حساب و هندسه استفاده میکردند. علم حساب با اعداد و محاسبه سر و کار دارد. در حساب، چهار عمل اصلی عبارتند از: جمع، تفریق، ضرب و تقسیم. هندسه علم مطالعه خطها، زاویهها، شکلها، و حجمها است. یونانیهایی چون اقلیدس، حدود ۲۵۰۰ سال قبل، بیشتر قوانین اصلی هندسه (قضایای هندسه) را تعیین کردند. جبر نوعی خلاصهنویسی ریاضیات است که در آن برای نشان دادن کمّیتهای نامعلوم، از علائمی چون x و y استفاده میشود. این علم را نیز دانشمندان ایرانی، حدود ۱۲۰۰ سال قبل توسعه دادند. حساب، هندسه و جبر، پایههای ریاضیات هستند.
ریاضیات نوعی زبان علمی است. مهندسان، فیزیکدانان، و سایر دانشمندان، همگی از ریاضیات در کارهایشان استفاده میکنند. سایر کارشناسان که به مطالعه اعداد، کمّیتها، شکلها و فضا بهشکل محض علاقه دارند، ریاضیات محض (غیرکاربردی) را به کار میگیرند. نظریه اعداد که شامل مطالعه اعداد درست و نحوه عمل آنهاست، شاخهای از ریاضیات محض به شمار میآید. در دنیای جدید، ریاضیات یکی از عناصر کلیدی علوم الکترونیک و رایانه بهشمار میرود.
کمیت
مجموعه، رابطه، تابع، عمل، گروه، میدان، عدد، اعداد طبیعی، اعداد حسابی، اعداد صحیح، اعداد اول، اعداد مرکب، اعداد گویا، اعداد گنگ، اعداد حقیقی، اعداد مختلط، اعداد جبری، عدد پی، عدد ای، چهارگانها، هشتگانها، شانزدگانها، اعداد پی-ادیک، اعداد فوق پیچیده (Hypercomplex numbers)، اعداد فوق حقیقی (Hyperreal number)، اعداد فراواقعی (Surreal numbers)، بینهایت، اعداد ترتیبی، اعداد اصلی، ثابتهای ریاضی، پایه
ساختار
جبر مجرد، نظریه اعداد، هندسه جبری، نظریه گروهها، مونوئیدها، آنالیز ریاضی، آنالیز تابعی، توپولوژی، جبر خطی، نظریه گراف، جبر عمومی، نظریه مدولها، نظریه ترتیب، [[نظ
فضا
توپولوژی، هندسه، مثلثات، هندسه جبری، هندسه دیفرانسیل، توپولوژی دیفرانسیل، توپولوژی جبری، جبر خطی، هندسه برخالها، متری
تغییر
حساب، حسابان، حساب برداری، آنالیز ریاضی، معادلات دیفرانسیل، سیستمهای دینامیکی، نظریه آشوب، فهرست تابعها
پایهها و روشهای ریاضیات
فلسفه ریاضیات، شهودگرایی، ساختگرائی، مبانی ریاضیات، نظریه مجموعهها، منطق نمادی، نظریه مدل، نظریه رستهها، منطق ریاضی، ریاضیات معکوس، جدول نمادهای ریاضی
ریاضیات گسسته
ترکیبیات، نظریه شهودی مجموعهها، نظریه رایانش، رمزنگاری، نظریه گراف
ریاضیات کاربردی
فیزیک ریاضی، مکانیک، مکانیک سیالات، آنالیز عددی، بهینهسازی، احتمالات، آمار، اقتصاد ریاضی، ریاضیات مالی، نظریه بازیها، ریاضیات زیستی، رمزنگاری، نظریه اطلاعات
گفتاورد (نقل قول)
برتراند راسل زمانی که دربارهٔ روش بُنداشتی (اصل موضوعی) سخن میگفت که در آن برخی ویژگیهای یک ساختار (که چیزی از آن نمیدانیم) فرض میشود و پیامدهای این فرض از راه منطق نتیجهگیری میشود گفت:
ریاضیات را میتوان رشتهای تعریف کرد که در آن نه معلوم است از چه سخن میگوییم و نه میدانیم آنچه میگوییم صحت دارد.
ما در ریاضیات مطالب را نمیفهمیم، بلکه تنها به آنها عادت میکنیم.





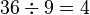


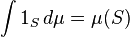


![[1,2,3][1,3,2]](https://upload.wikimedia.org/math/4/0/9/40921055cf207b7cd9919e7d89040ddb.png)
![[2,1,3][2,3,1]](https://upload.wikimedia.org/math/5/3/5/53588173bda96050a999469de6e4686c.png)
![[3,1,2][3,2,1]](https://upload.wikimedia.org/math/4/4/e/44e01a46c64150417955a1a4dc0ff240.png)